What is Equality?
Veterans
of our SDG (Science
Discussion Group – which met regularly in Aberdeen) will recall having
constructed the first of the two transformations of a point along a line shown below. All such transformations are mediated by
conics; the first transformation depicted below is mediated by a pair of
straight lines—which is one of the two conic sections made by a plane cutting a
right, circular cone through its vertex: the other is a point.
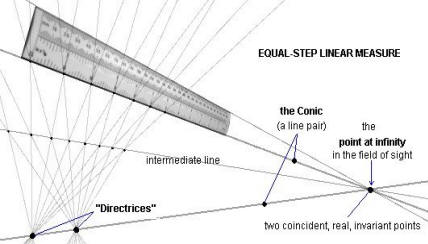 There are always two
so-called “invariant” points on the transforming line. Invariants cannot be transformed
(moved). They can both be real, or both
imaginary. If they are real, they can be
either distinct, or, as on the left, co-incident.
In the construction, they are co-incident where the parallel edges of
the ruler meet, namely at infinity. This point happens to be in our field of
view. If this point were as far out of view as possible, then the ruler’s
intervals would seem equal in the accustomed way. (Try this with a physical ruler: look
squarely at it, then askance along it. Do note there is no abrupt discontinuity
between these views.)
There are always two
so-called “invariant” points on the transforming line. Invariants cannot be transformed
(moved). They can both be real, or both
imaginary. If they are real, they can be
either distinct, or, as on the left, co-incident.
In the construction, they are co-incident where the parallel edges of
the ruler meet, namely at infinity. This point happens to be in our field of
view. If this point were as far out of view as possible, then the ruler’s
intervals would seem equal in the accustomed way. (Try this with a physical ruler: look
squarely at it, then askance along it. Do note there is no abrupt discontinuity
between these views.)
Now,
it would appear that we will get equal steps of translation along a line if,
and only if, this co-incident pair
of real invariants lies precisely in or
at the infinite on that line, as the match of the geometry to the
ruler seems to show.
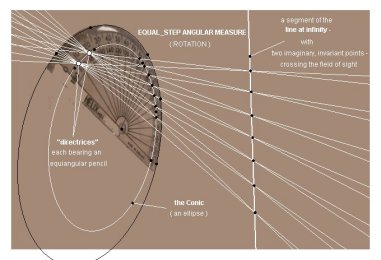 The
second construction is probably new to most of us. It is like the
first, in that a point is being transformed along a line via a conic in exactly
the same way, but here the conic is an ellipse—and the line bearing the
transforming point misses it. This means
that the two invariants are imaginary.
The
second construction is probably new to most of us. It is like the
first, in that a point is being transformed along a line via a conic in exactly
the same way, but here the conic is an ellipse—and the line bearing the
transforming point misses it. This means
that the two invariants are imaginary.
The
main effect of this on the transformation
is that, because there are no real
invariants to ‘get in the way’, all the (real) points of the line
can be moved, and iterated indefinitely—in fact, cyclically, round and round,
so this style of transformation ideally suits rotation, and can provide
a stepping measure of it. Now, we will by
this iteration get equiangular steps
only
if the transforming point always lies in the infinite, as the match,
here, to a photograph of an actual, physically-extant protractor seems to show:
outgoing and incoming lines through a point in the line, from and to the
directrices, are parallel chords of the conic, and so must meet in the
infinite. And all such points must lie
in the one ‘line at infinity’ of the conic’s plane.
Thus
it would seem that equality, and with it the
ability to calibrate (or, to coin
a phrase, “to unitise”)
both translation and rotation, depend intimately on certain
relationships with infinite elements. Accordingly, in order for us to be sure that our
intervals are absolutely equal,
we need to be sure that infinity is absolutely
locatable.
What is Equality? page 2
·
I
expect that most of us accept that N mutually parallel lines all have the
same orientation.
·
And
we will accept that all N of them meet in the same point at infinity.
·
And
we further accept that another
set of such parallels (on the same plane as the first set) with a different
orientation must meet in a different point at infinity.
·
Finally,
we accept that the line drawn through
these two, different points at infinity must pass through the points at infinity
selected by pairs of parallels on the plane of those parallels.
So, if we can find two such pairs of
absolutely
parallel lines,
we
can find the absolute line at infinity.
Let us try it!
The
photograph
on the left, below, of lines drawn on a plane, contains two such pairs of
parallels. Find them, and mark
them.
The photograph on the right, below, of
conics drawn on a plane, contains two circles. Find and mark them.


It should dawn on us
that parallelity and circularity are never preserved under projection.
Since
spatial measurement, even physical measurement,
always
involves projection*, it follows from the foregoing that we can never be sure of finding absolute infinity, and in
consequence cannot detect absolute equality.
I venture to suggest that this changes everything!
*
If you doubt this, try using a ruler
to measure something in total darkness!